Density, distribution function, quantile function, and random generation for the transition probabilities in the Cox-Ingersoll-Ross process given by the stochastic differential equation dX = lambda*(xi-X)*dt + gamma*sqrt(X)*dB (interpreted in the sense of Ito (default) or Stratonovich (optional))
dCIR(x,x0,lambda,xi,gamma,t,Stratonovich=FALSE,log=FALSE)
pCIR(x,x0,lambda,xi,gamma,t,Stratonovich=FALSE,log.p=FALSE,lower.tail=TRUE)
qCIR(p,x0,lambda,xi,gamma,t,Stratonovich=FALSE,log.p=FALSE,lower.tail=TRUE)
rCIR(n,x0,lambda,xi,gamma,t,Stratonovich=FALSE)Arguments
- x, q
Target state, assumed >= 0
- x0
Initial state, assumed > 0
- lambda
Rate parameter, assumed > 0
- xi
Mean parameter, assumed > 0
- gamma
Noise intensity parameters, assumed > 0
- t
Terminal time, assumed > 0
- Stratonovich
Logical, TRUE for Stratonovich, FALSE (default) for Ito
- log, log.p
Logical, if TRUE, probabilities/densities are given as log(p). Default is FALSE
- lower.tail
Logical; if TRUE (default) probabilities are P(X<=x); otherise, P(X>x).
- p
Probability, assumed >= 0 and <= 1.
Value
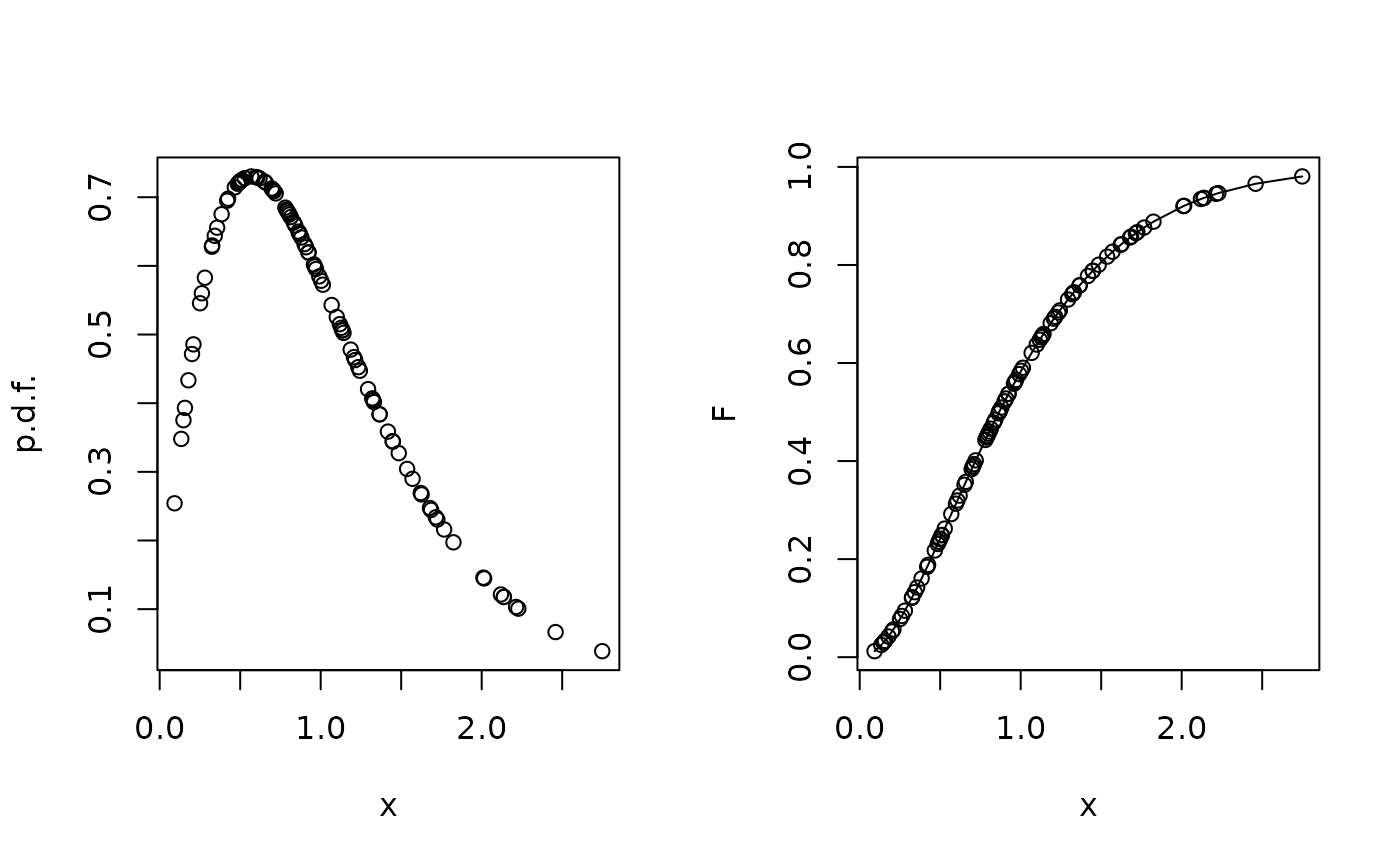
dCIR gives the transition probability density, pCIR gives the distribution of the transitio probability, qCIR gives the quantiles, and rCIR samples a random terminal point.
The length of the result is determined by n for rCIR, and is the maximum of the lengths of the numerical arguments for the other functions.