This R package provides functionality for stochastic differential equations in terms of:
- Simulating sample paths
- Computing transition probabilities numerically in 1 and 2 dimensions
- Estimating states (and parameters) for 1D or 2D equations, using Hidden Markov Model methods.
- Solve optimal control problems numerically, using Markov Decision Process machinery.
The package supports the textbook (Thygesen 2023) by implementing algorithms described in the book, so it provides the computational framework to accompany the theory. It has been used to produce almost all figures in the book.
Installation
To install the package, open R and run
devtools::install_github("Uffe-H-Thygesen/SDEtools")Alternatively, clone the github repo to your local machine and “make install” it, if you are familiar with make and makefiles.
Then load the package with
Example
This is a basic example which shows you how to simulate a sample path, and compute the transition probability, for a double well model:
library(SDEtools)
## The double well model is dX = f(X)*dt + g(X)*dB with:
f <- function(x) x-x^3
g <- function(x) 0.5
## Define a time grid and simulate the process
tv <- seq(0,100,0.1)
sim <- heun(f,g,tv,0)
plot(tv,sim$X,type="l",ylim=c(-1.5,1.5))
## Compute the stationary density using a spatial grid
xi <- seq(-1.5,1.5,0.01)
xc <- cell.centers(xi)
## Define the diffusivity
D <- function(x) 0.5*g(x)^2
## Compute the generator
G <- fvade(f,D,xi,'r')
#> Loading required package: Matrix
## Compute the stationary distribution
rho <- StationaryDistribution(G)
## Rescale and add to the plot
lines(20*rho/max(rho),xc)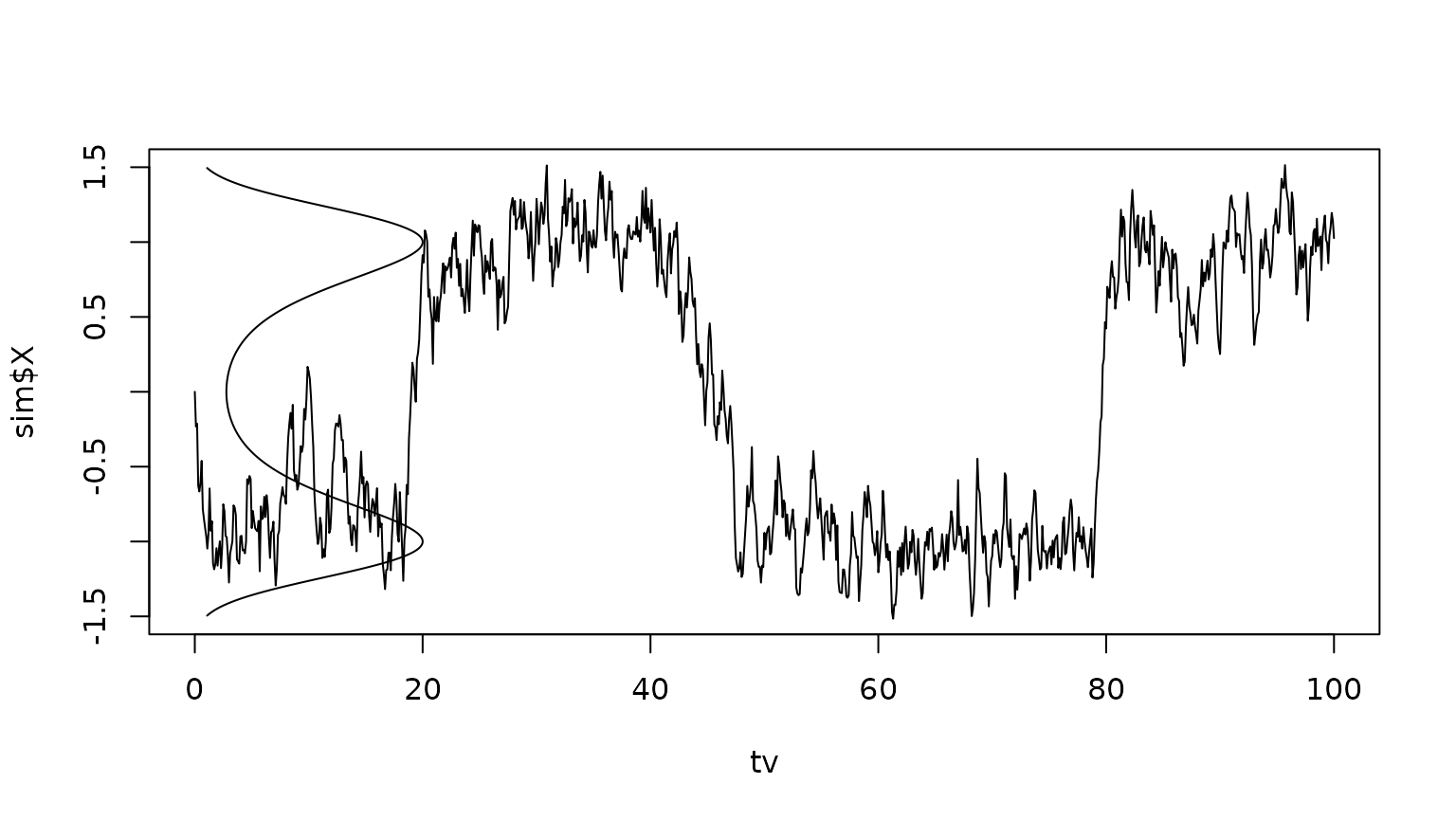
References
Thygesen, Uffe Høgsbro. 2023. Stochastic Differential Equations for
Science and Engineering. Taylor & Francis. http://uffe-h-thygesen.github.io.