fvade discretizes the advection-diffusion equation
dC/dt = -(u*C-D*C')'
on an interval [a,b] using the finite-volume method. A loss term can be included, as in
dC/dt = -(u*C-D*C')' - r*C
fvade(u, D, xgrid, bc, sparse = TRUE, diagonals = FALSE, r = NULL)Arguments
- u
function mapping state (numeric scalar) to advective term (numeric scalar)
- D
function mapping state (numeric scalar) to diffusivity (numeric scalar)
- xgrid
The numerical grid. Numeric vector of increasing values, giving cell boundaries
- bc
String indicating boundary conditions. See details.
- sparse
logical indicating if the result should be returned as a sparse matrix
- diagonals
logical indicating if the result should be returned as a list of subdiagonal, diagonal, and superdiagonal
- r
function mapping state (numeric scalar) to mortality/discount rate. Defaults to 0.
Value
a quadratic matrix, the (sub)generator of the approximating continuous-time Markov chain, with length(xgrid)-1 columns
Details
Handling of boundary conditions: Input argument bc is a single character, or a vector of two characters, coding the condition at each boundary as follows: 'r': Reflecting boundary 'p': Periodic boundaries: Exit at this boundary to re-enter at the other 'a': Absorbing boundaries. In this case G will be a sub-generator 'c': Continue beyond boundary (experimental; read the source) 'e': Return generator, Extended to include absorbing boundaries
Return value: The function fvade returns a generator (or sub-generator) G of a continuous-time Markov Chain. This chain jumps between cells defined by xgrid. When using the generator to solve the Kolmogorov equations, note that G operates on probabilities of each cell, not on the probability density in each cell. The distinction is particularly important when the grid is non-uniform.
Examples
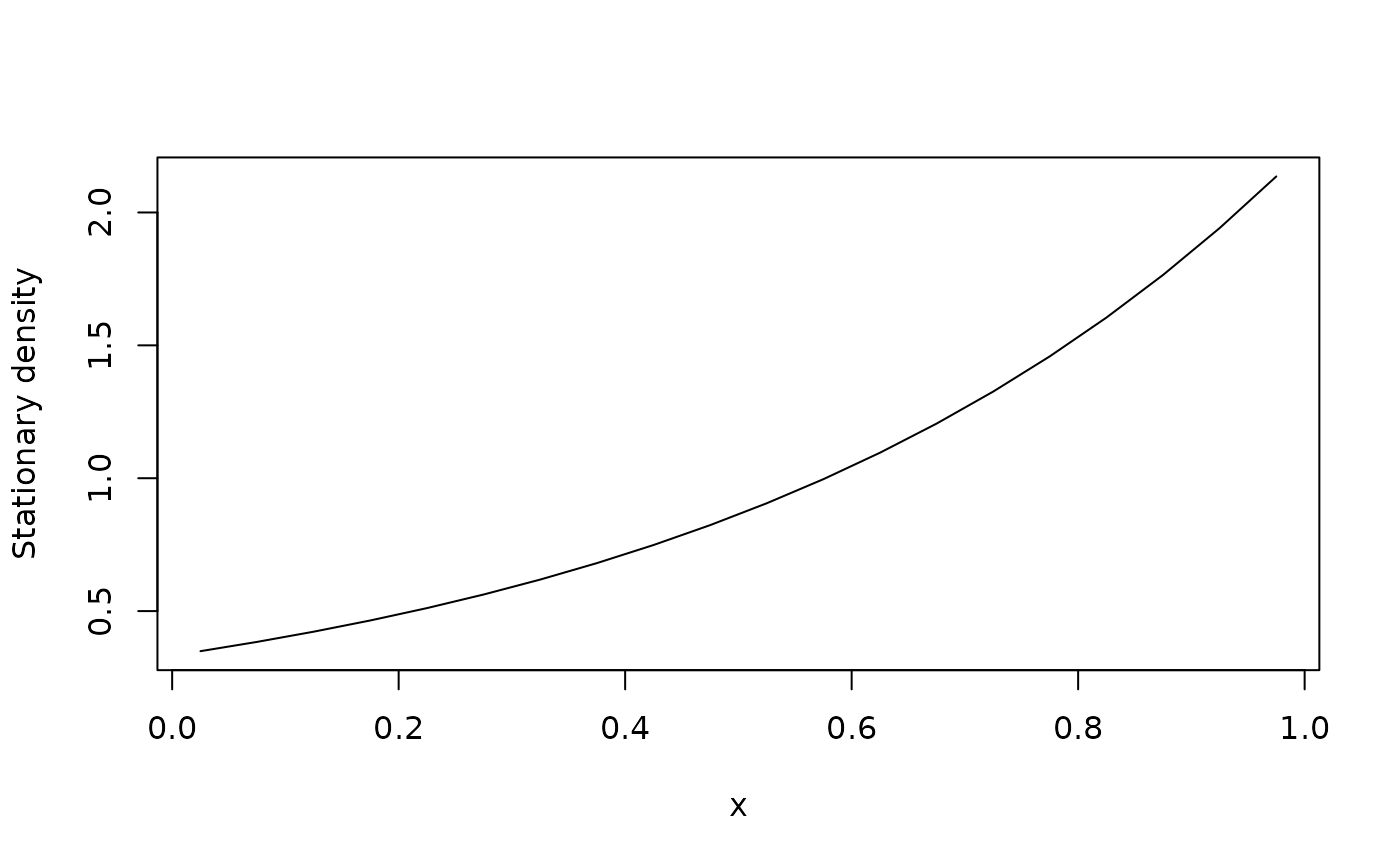
# Generator of standard Brownian motion with unit drift on the unit interval, reflecting boundaries
xi <- seq(0,1,0.05) # Cell boundaries
dx <- diff(xi) # Cell widths
xc <- xi[-1] - 0.5*dx # Cell centers
G <- fvade(function(x)1,function(x)0.5,seq(0,1,0.05),'r')
# Find the density of the stationary distribution
phi <- StationaryDistribution(G) # Find stationary probabilities
phi <- phi/dx # Convert to densities
plot(xc,phi,type="l",xlab="x",ylab="Stationary density")