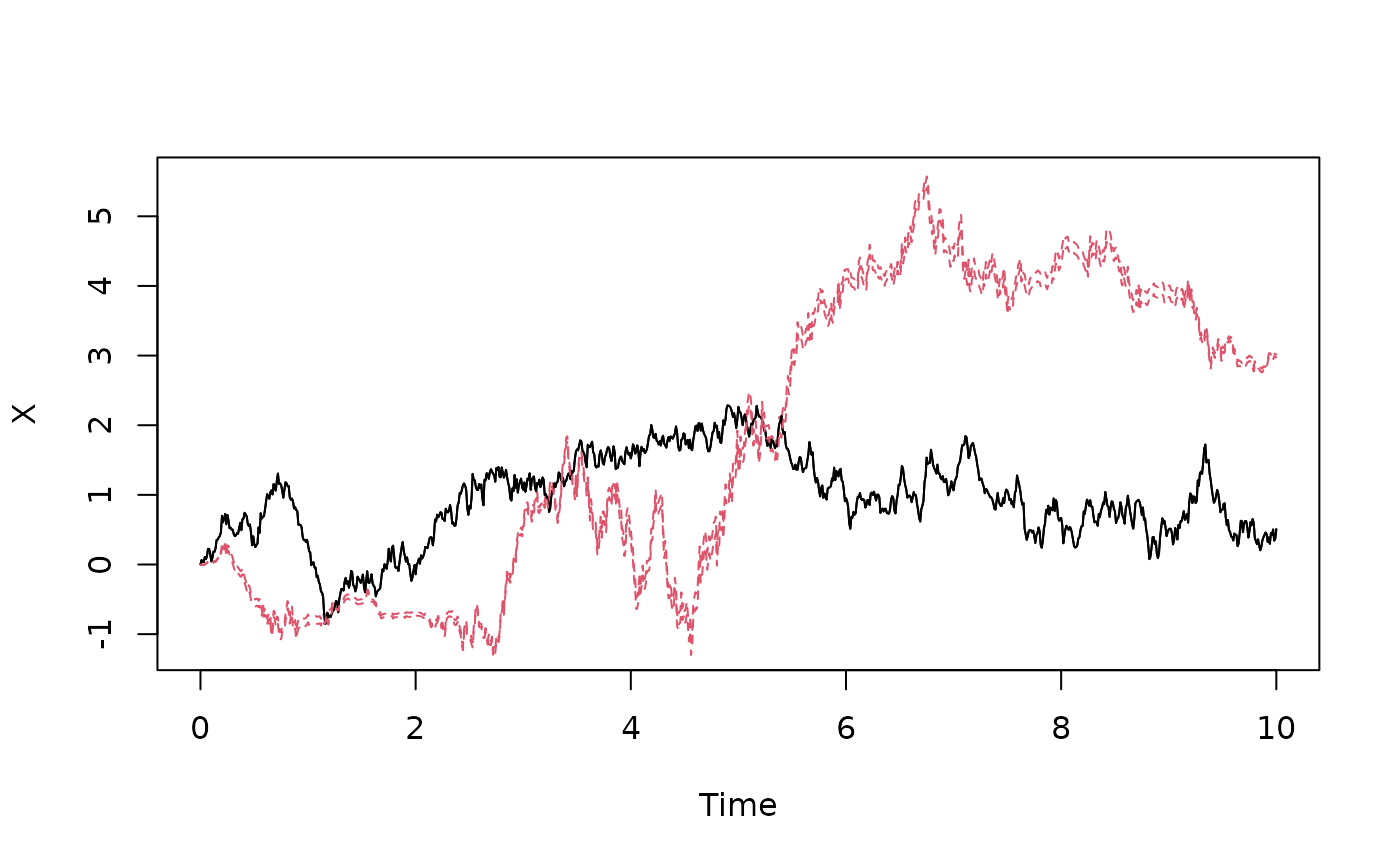Heun's method for simulation of a Stratonovich stochastic differential equation dX = f dt + g dB
Source:R/sdetools.R
heun.RdHeun's method for simulation of a Stratonovich stochastic differential equation dX = f dt + g dB
heun(
f,
g,
times,
x0,
B = NULL,
p = function(x) x,
h = NULL,
r = NULL,
S0 = 1,
Stau = runif(1)
)Arguments
- f
function f(x) or f(t,x) giving the drift term in the SDE
- g
function g(x) or g(t,x) giving the noise term in the SDE
- times
numeric vector of time points, increasing
- x0
numeric vector giving the initial condition
- B
sample path of (multivariate) Browniań motion. If omitted, a sample is drawn using rvBM
- p
Optional projection function that at each time poins projects the state, e.g. to enforce non-negativeness
- h
Optional stopping function; the simulation terminates if h(t,x)<=0
Examples
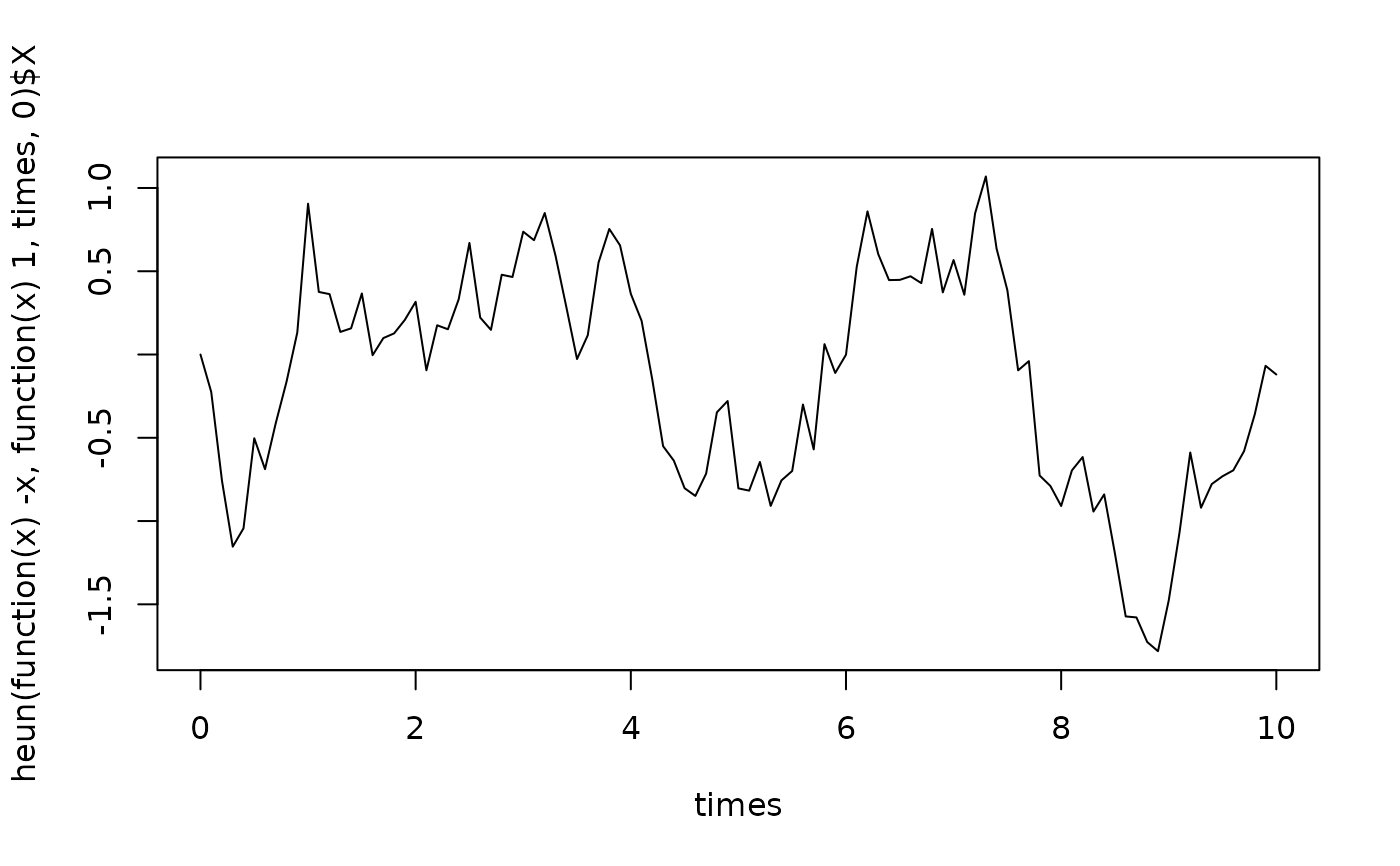
times <- seq(0,10,0.1)
# Plot a sample path of the solution of the SDE dX=-X dt + dB
plot(times,heun(function(x)-x,function(x)1,times,0)$X,type="l")
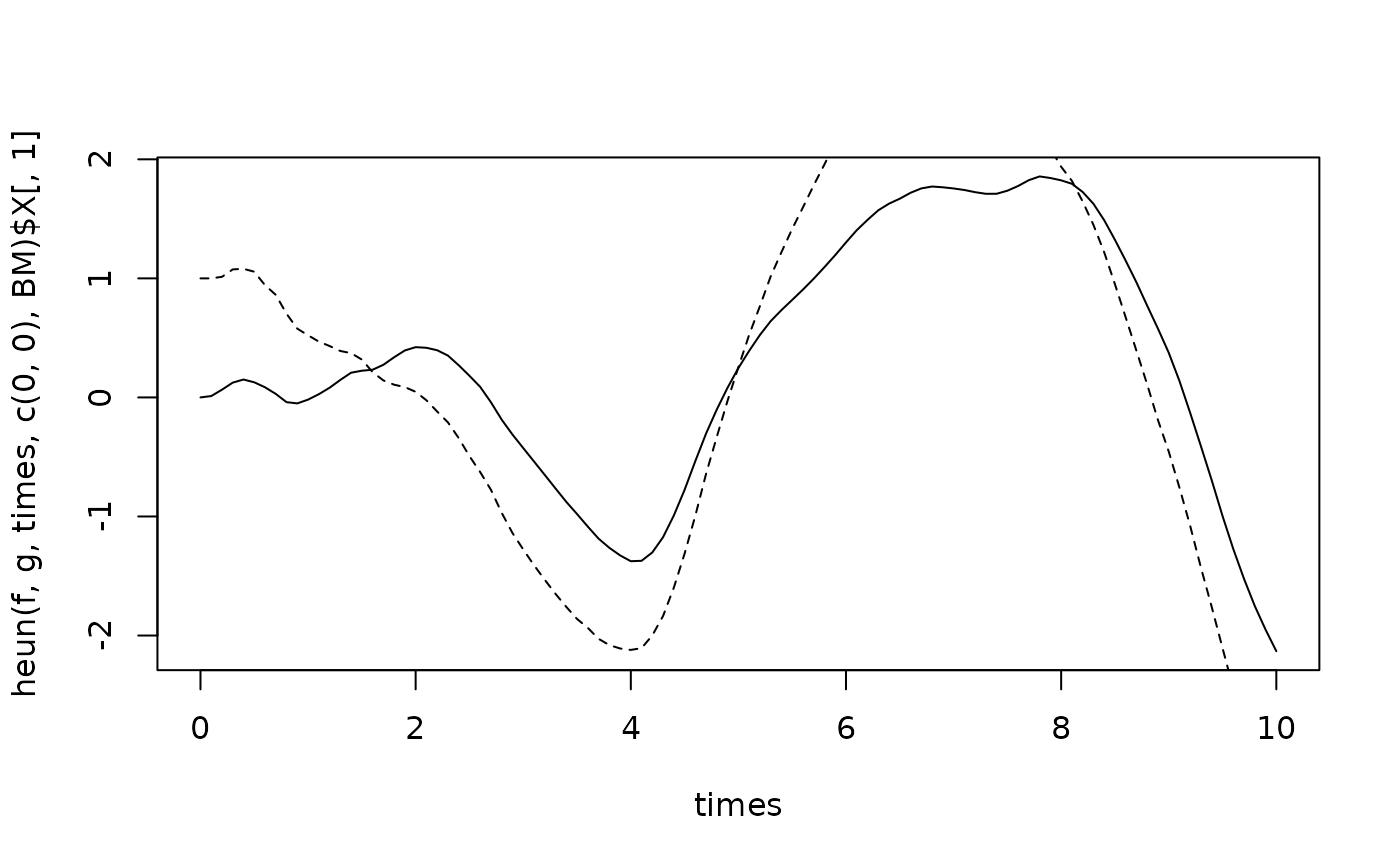
 # Plot a sample path of the solution of the 2D time-varying SDE dX=(AX + FU) dt + G dB
A <- array(c(0,-1,1,-0.1),c(2,2))
F <- G <- array(c(0,1),c(2,1))
f <- function(t,x) A %*% x + F * sin(2*t)
g <- function(x) G
BM <- rBM(times)
plot(times,heun(f,g,times,c(0,0),BM)$X[,1],type="l")
# Add solution corresponding to different initial condition, same noise
lines(times,euler(f,g,times,c(1,0),BM)$X[,1],type="l",lty="dashed")
# Plot a sample path of the solution of the 2D time-varying SDE dX=(AX + FU) dt + G dB
A <- array(c(0,-1,1,-0.1),c(2,2))
F <- G <- array(c(0,1),c(2,1))
f <- function(t,x) A %*% x + F * sin(2*t)
g <- function(x) G
BM <- rBM(times)
plot(times,heun(f,g,times,c(0,0),BM)$X[,1],type="l")
# Add solution corresponding to different initial condition, same noise
lines(times,euler(f,g,times,c(1,0),BM)$X[,1],type="l",lty="dashed")
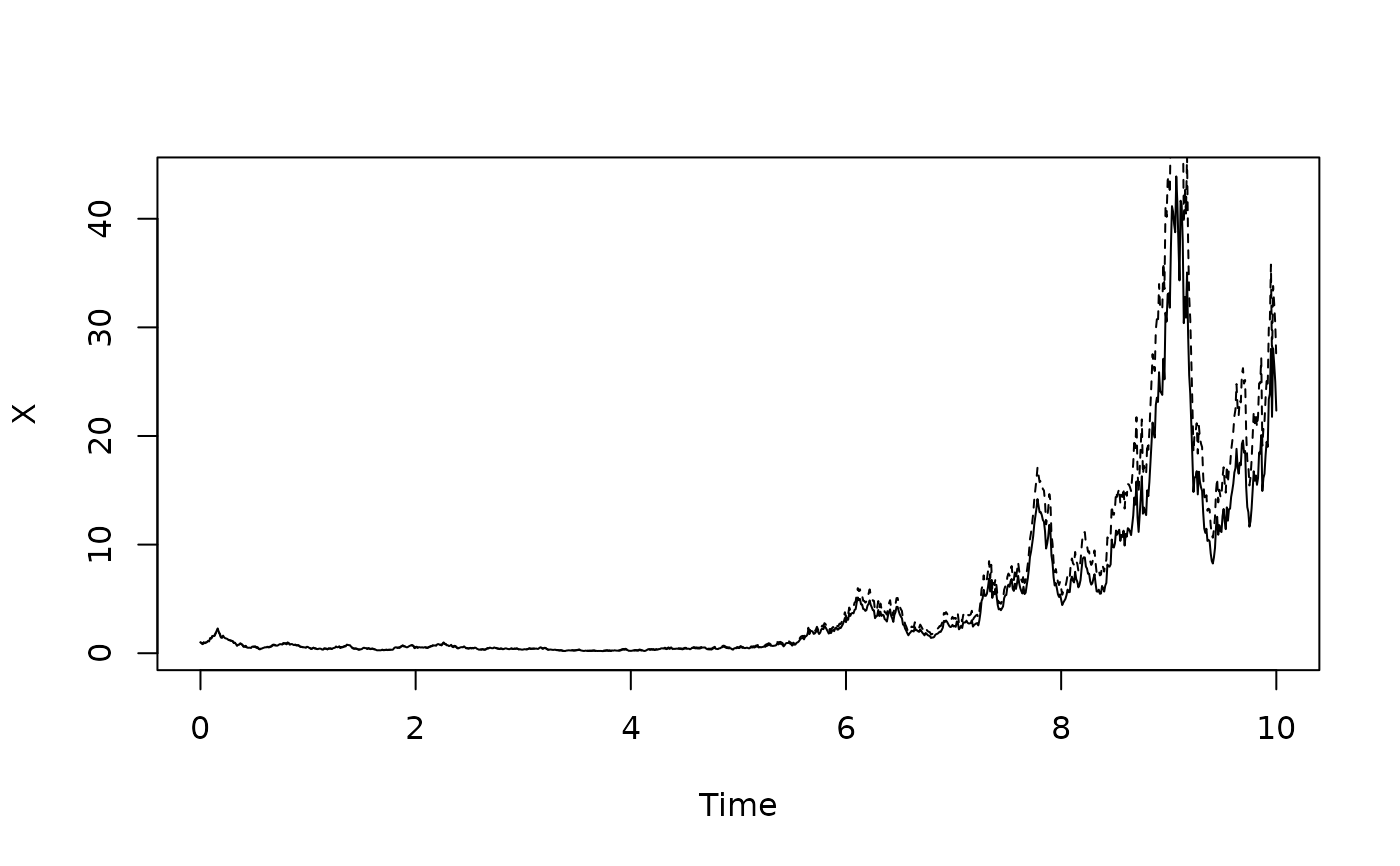
 # Solve geometric Brownian motion as a Stratonovich equation
times <- seq(0,10,0.01)
BM <- rBM(times)
plot(times,heun(function(x)-0.1*x,function(x)x,times,1,BM)$X,type="l",xlab="Time",ylab="X")
# Add solution of corresponding Ito equation
lines(times,euler(function(x)0.4*x,function(x)x,times,1,BM)$X,lty="dashed")
# Solve geometric Brownian motion as a Stratonovich equation
times <- seq(0,10,0.01)
BM <- rBM(times)
plot(times,heun(function(x)-0.1*x,function(x)x,times,1,BM)$X,type="l",xlab="Time",ylab="X")
# Add solution of corresponding Ito equation
lines(times,euler(function(x)0.4*x,function(x)x,times,1,BM)$X,lty="dashed")
 # Testing a case with non-commutative noise
BM2 <- rvBM(times,2)
matplot(times,heun(function(x)0*x,
function(x)diag(c(1,x[1])),times,c(0,0),BM2)$X,xlab="Time",ylab="X",type="l")
# Add solution to the corresponding Ito equation
matplot(times,euler(function(x)0*x,
function(x)diag(c(1,x[1])),times,c(0,0),BM2)$X,xlab="Time",ylab="X",type="l",add=TRUE)
# Testing a case with non-commutative noise
BM2 <- rvBM(times,2)
matplot(times,heun(function(x)0*x,
function(x)diag(c(1,x[1])),times,c(0,0),BM2)$X,xlab="Time",ylab="X",type="l")
# Add solution to the corresponding Ito equation
matplot(times,euler(function(x)0*x,
function(x)diag(c(1,x[1])),times,c(0,0),BM2)$X,xlab="Time",ylab="X",type="l",add=TRUE)