Integrate one sample path of a stochastic process w.r.t. another, returning the Ito integral, the Stratonovich integral, or the "right hand rule".
Source:R/sdetools.R
stochint.RdIntegrate one sample path of a stochastic process w.r.t. another, returning the Ito integral, the Stratonovich integral, or the "right hand rule".
stochint(f, g, rule = "l")Arguments
Value
A numeric vector, same length as f, giving the "running integral", i.e. the integral as a function of the upper limit.
Examples
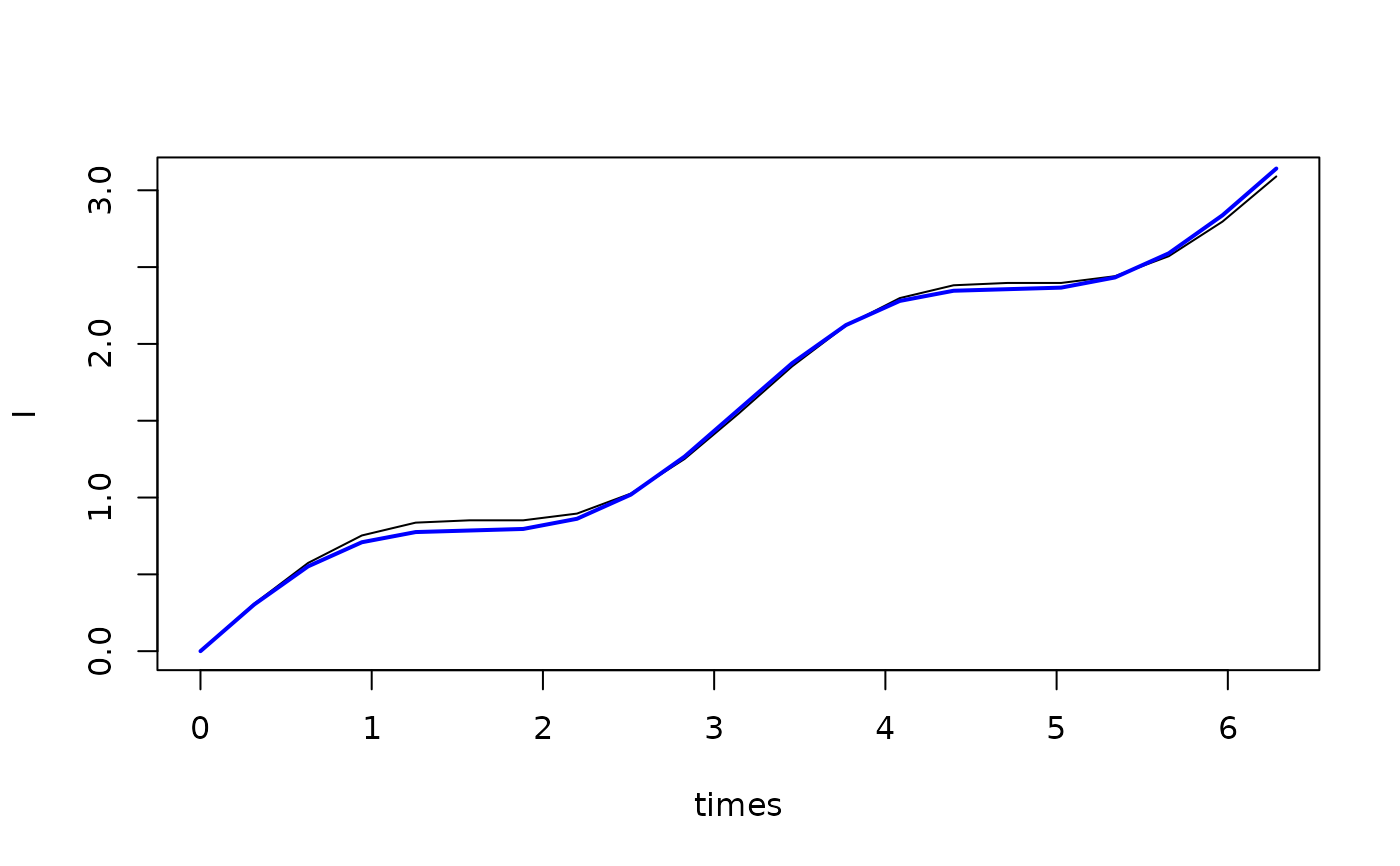
## Integrating a cosine w.r.t. a sine
times <- seq(0,2*pi,length=21)
I <- stochint(cos(times),sin(times))
Ia <- 0.5*times+0.25*sin(2*times) # Analytical result
matplot(times,I,type="l")
lines(times,Ia,col="blue",lwd=2)
 ## Integration of Brownian motion w.r.t. itself
times <- seq(0,10,0.01)
BM <- rBM(times)
I <- stochint(BM,BM,c("l","c","r"))
matplot(times,cbind(I$l,0.5*BM^2-0.5*times),type="l",xlab="Time",ylab="Left integral (Ito)",
main="Integral of B.M. w.r.t itself")
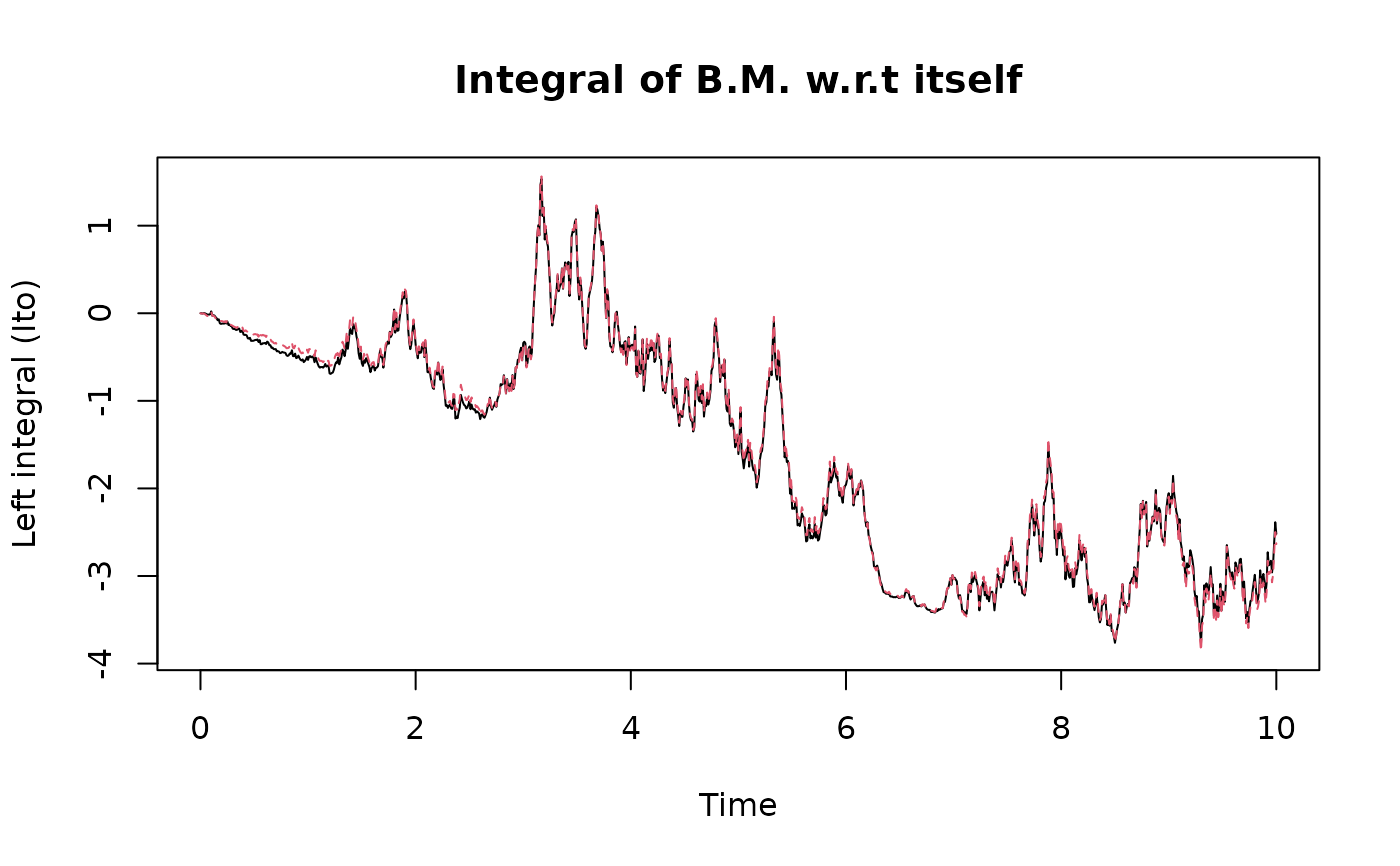
## Integration of Brownian motion w.r.t. itself
times <- seq(0,10,0.01)
BM <- rBM(times)
I <- stochint(BM,BM,c("l","c","r"))
matplot(times,cbind(I$l,0.5*BM^2-0.5*times),type="l",xlab="Time",ylab="Left integral (Ito)",
main="Integral of B.M. w.r.t itself")
 matplot(times,cbind(I$r,0.5*BM^2+0.5*times),type="l",xlab="Time",ylab="Right integral",
main="Integral of B.M. w.r.t itself")
matplot(times,cbind(I$r,0.5*BM^2+0.5*times),type="l",xlab="Time",ylab="Right integral",
main="Integral of B.M. w.r.t itself")
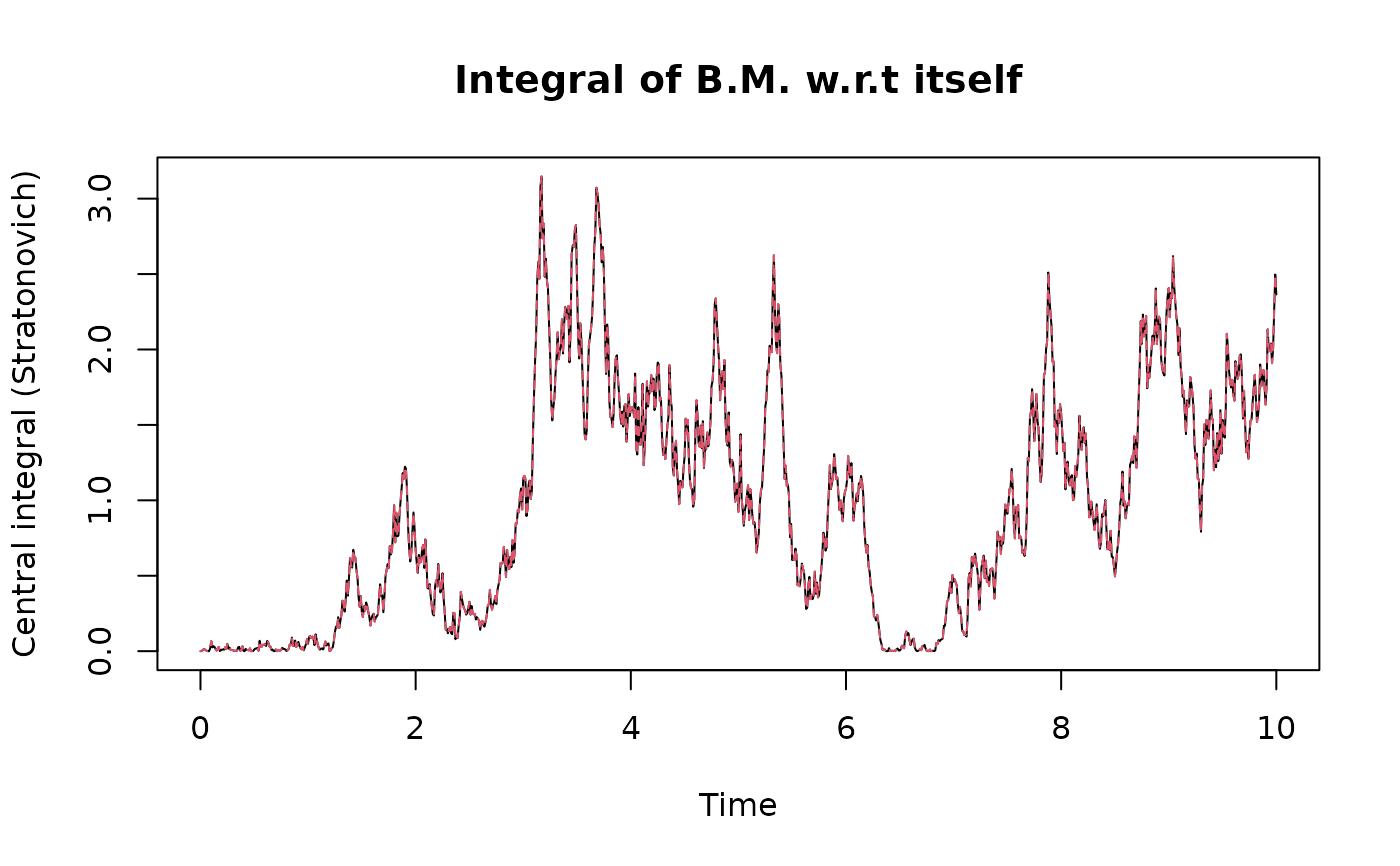
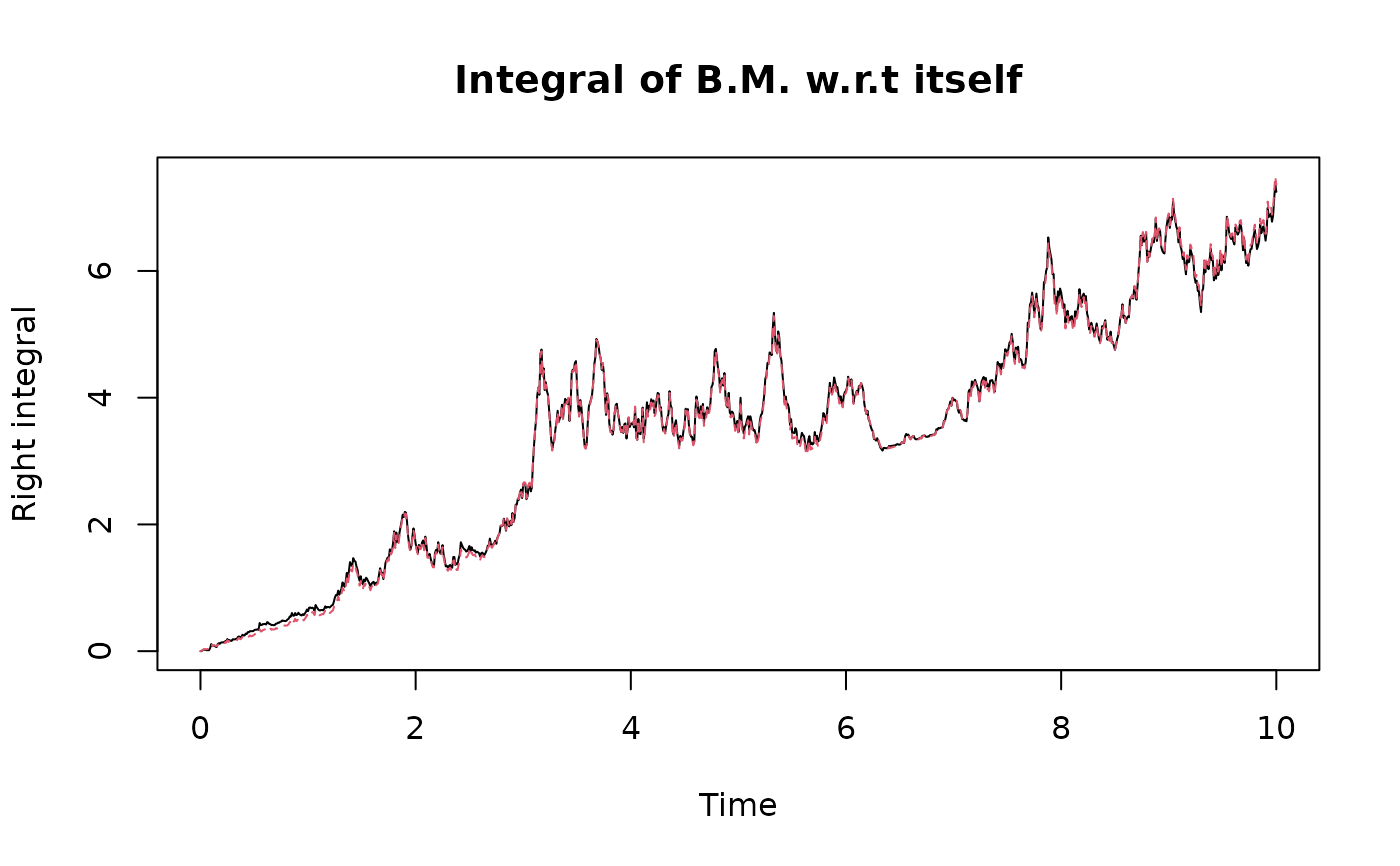 matplot(times,cbind(I$c,0.5*BM^2),type="l",xlab="Time",ylab="Central integral (Stratonovich)",
main="Integral of B.M. w.r.t itself")
matplot(times,cbind(I$c,0.5*BM^2),type="l",xlab="Time",ylab="Central integral (Stratonovich)",
main="Integral of B.M. w.r.t itself")