Solve the optimal control problem using policy iteration, i.e. find the optimal strategy and value function for the case where the uncontrolled system is given by a subgenerator G0 (either due to discounting or due to absorbing boundaries)

PolicyIterationRegular(
  G0,
  G1,
  k,
  uopt,
  iter.max = 1000,
  tol = 1e-12,
  do.minimize = TRUE,
  do.return.QSD = FALSE
)

Arguments

G0: The sub-generator of the uncontrolled system
G1: A list of (sub-)generators for each control
k: The running cost
uopt: A list of functions returning optional controls in each state. See details.
iter.max: = 1000 Maximum number of iterations
tol: = 1e-12 Tolerance for convergence
do.minimize=TRUE: Is the optimization problem one of minimization (and not maximization)?
do.return.QSD=FALSE: Compute and return the quasi-stationary distribution

Value

A list containing

V: The value function, as a vector with an element for each state

u: The optimal controls, as a matrix with a row for each state and a column for each control

If do.return.QSD==TRUE, also:

qsd.value: The decay rate of the quasi-stationary distribution

qsd.vector: The quasi-stationary distribution

Details

Specifying optimal controls: Each control variable has an element in the list G1 of (sub)generators, and an element in the list uopt of optimal controls.

The function uopt[[i]] is applied to G1[[i]]*V, where V is the value function. The result is the optimal value of the control, in each possible state.

The final generator for the controlled system is obtain as G0 + sum(Diagonal(u[[i]])*G1[[i]]) where the sum is over the controls i.

Examples

## Controlling a system to the boundary with minimum effort
H <- 2
xi <- seq(-H,H,length=201)
xc <- as.numeric(cell.centers(xi,c(0,1))$x)
dx <- diff(xi)

G0 <- fvade(function(x)0,function(x)0.5,xi,'a')
#> Loading required package: Matrix
Gp <- fvade(function(x)1,function(x)0,xi,'a')   # Going right 
Gn <- fvade(function(x)-1,function(x)0,xi,'a')  # Going left

# The payoff - time plus control effort
k <- function(u) 0.5 + 0.5*u[,1]^2 + 0.5*u[,2]^2

# For each control, the optimal u maximizes Li V*u + k over [0,Inf)
# Here, going right corresponds to Lp V = V' while going left corresponds to
# Ln V = -V'
uopt <- function(dV)pmax(0,-dV)

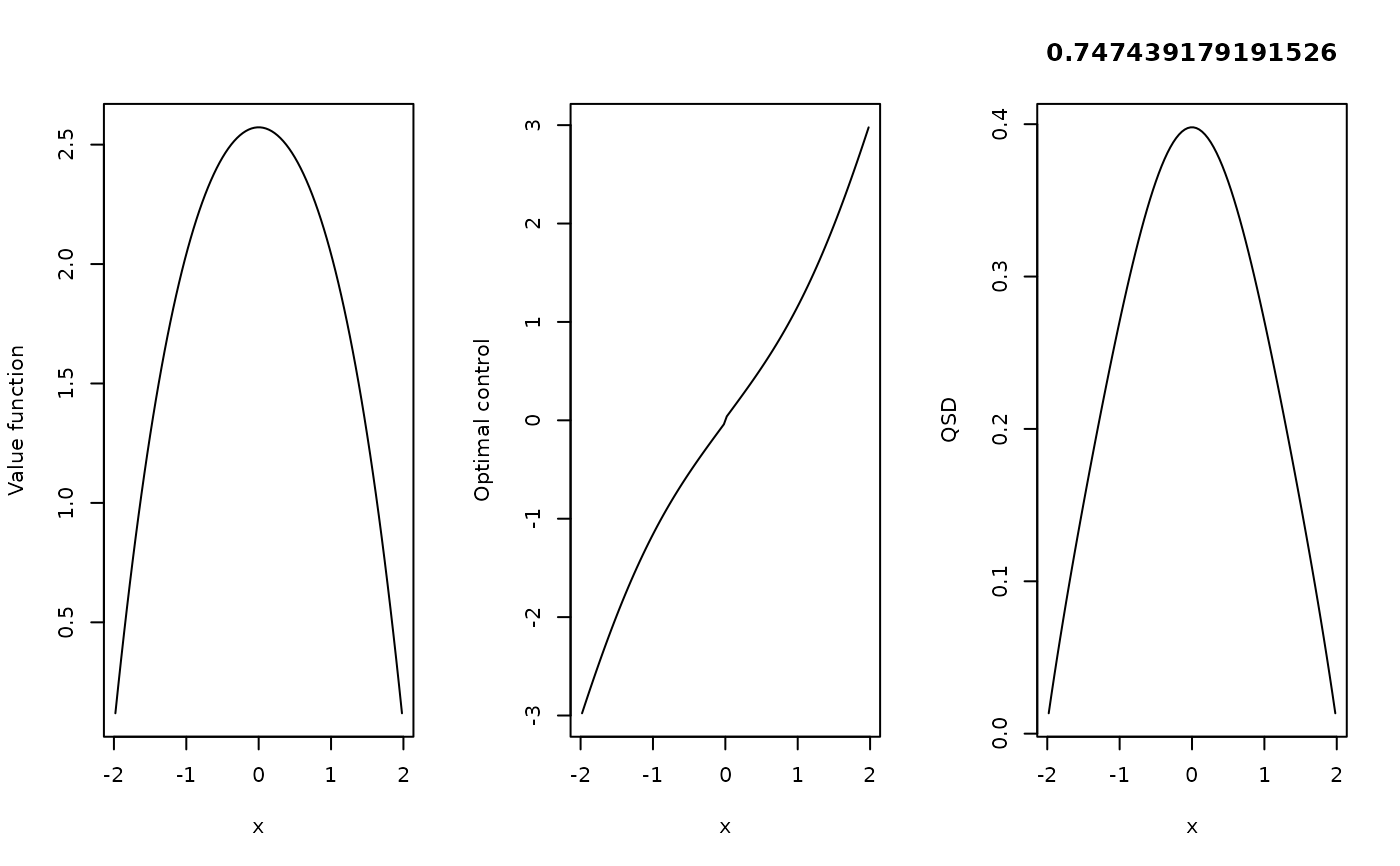
sol <- PolicyIterationRegular(G0,list(Gp,Gn),k,list(uopt,uopt),do.return.QSD=TRUE)

par(mfrow=c(1,3))
plot(xc,sol$V,xlab="x",ylab="Value function")
lines(xc,log(cosh(H)/cosh(xc)))
plot(xc,sol$u[,1]-sol$u[,2],xlab="x",ylab="Optimal control")
lines(xc,tanh(xc))
plot(xc,sol$qsd.vector/dx,type="l",xlab="x",ylab="QSD",main=sol$qsd.value)