Solve the optimal control problem using policy iteration, i.e. find the optimal strategy and value function for the case where the uncontrolled system is given by a generator G0

PolicyIterationSingular(
  G0,
  G1,
  k,
  uopt,
  iter.max = 1000,
  tol = 1e-12,
  do.minimize = TRUE
)

Arguments

G0: The generator of the uncontrolled system
G1: A list of generators for each control
k: The running cost
uopt: A list of functions returning optional controls. See details.
iter.max: = 1000 Maximum number of iterations
tol: = 1e-12 Tolerance for convergence
do.minimize=TRUE

Value

A list containing V: The value function, as a vector with an element for each state u: The optimal controls, as a matrix with a row for each state and a column for each control pi: The stationary distribution for the controlled system gamma: The expected running cost in stationarity

Details

Specifying optimal controls: Each control variable has an element in the list G1 of generators, and an element in the list uopt of optimal controls.

The function uopt[[i]] is applied to G1[[i]]*V, where V is the value function. The result is the optimal value of the control, in each possible state.

The final generator for the controlled system is obtain as G0 + sum(Diagonal(u[[i]])*G1[[i]]) where the sum is over the controls i.

Examples

require(SDEtools)

## Fisheries management dX = X*(1-X)*dt - U*dt + sigma*X*dB
sigma <- 0.5
## Rewrite in advection-diffusion form
D <- function(x) 0.5*sigma^2*x^2
Dp <- function(x) sigma^2*x
u <- function(x) x*(1-x) - Dp(x)

# Spatial grid - concentrated around 0
xi <- seq(0,sqrt(3),length=201)^2
xc <- 0.5*(head(xi,-1) + tail(xi,-1))

# Generator for the unfished system, and for fishing
G0 <- fvade(u,D,xi,'r')
G1 <- fvade(function(x)-1,function(x)0,xi,'r')

# Pay-off function
k <- function(u) sqrt(u)

# Optimal control - really 1/4/V'(x)^2, but avoid V'<=0, and do not
# fish in the lowest element in state space, to avoid degeneracies
uopt <- function(dV) { u <- 0.25/pmax(1e-6,-dV)^2; u[1] <- 0 ; return(u)}

sol <- PolicyIterationSingular(G0,list(G1),k,list(uopt),do.minimize=FALSE)

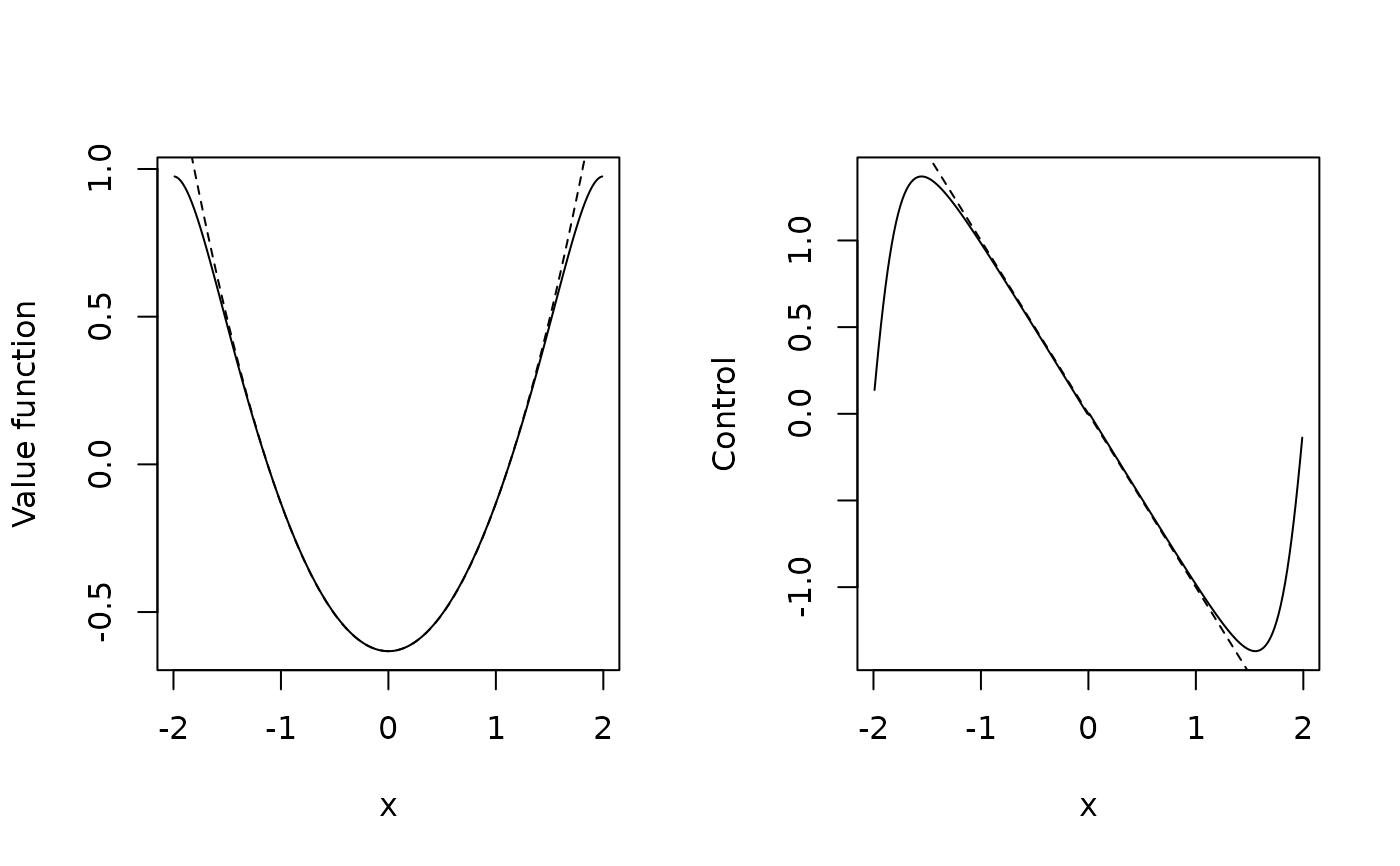
# Plots comparing with analytical solution: V(x) = 0.5*log(x), u(x)=x^2
par(mfrow=c(1,2))
i1 <- sum(xi<1) # Identify state corresponding to x=1, for shifting V
plot(xc,0.5*log(xc),type="l",ylim=c(-2,0.6),xlab="x",ylab="Value function")
points(xc,sol$V - sol$V[i1])
plot(xc,xc^2,type="l",xlab="x",ylab="Control")
points(xc,sol$u)